磨料磨具网

       引言

       麻花钻头生产的两个主要磨削步骤为排屑槽磨削和后刀面磨削，其磨削参数决定了钻头的几何参数。像顶角和钻芯厚度等就是钻头制造参数的隐函数。

       在排屑槽磨削中，砂轮原地旋转，同时钻头绕轴旋转并向下移动。钻头的这种双重运动控制着排屑槽的螺旋角和位置，而砂轮的断面形状则控制着排屑槽的横剖面。上述磨削步骤以正交位置进行两次就生产出双排屑槽钻头。在后刀面磨削中，砂轮绕着固定轴旋转形成一个圆锥半角θ的磨锥（图1所示），钻头绕着磨锥轴旋转。以上磨削步骤以对称位置进行两次就生产出双后刀面。这些侧面可以看成是磨锥的截面。

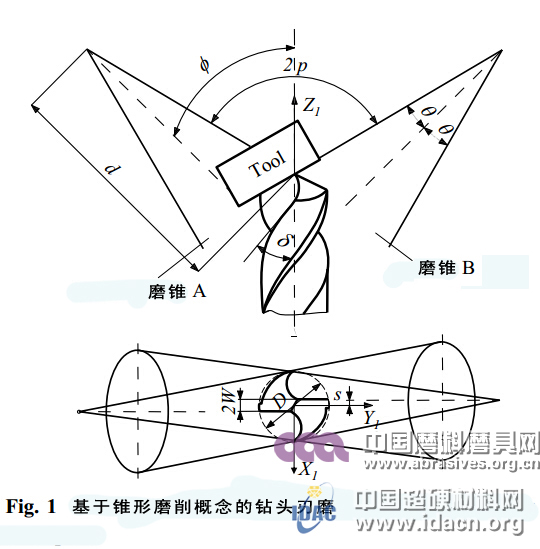
       本研究利用计算机辅助设计（CAD）对钻槽生产中的砂轮设计进行研究。利用MATLAB工具进行CAD建模，并得出实验结果和讨论。

       实验方法

       1. 建立坐标系和设置变量

       为了对排屑槽设计轮廓、钻头螺旋沟槽面和砂轮断面形状进行建模，建立如图2所示的坐标系。
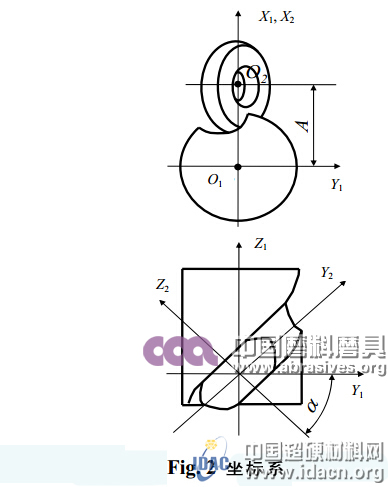
       钻头螺旋沟槽坐标O1—X1Y1Z1设置为移动坐标，砂轮坐标O2—X2Y2Z2设置为固定坐标。

       研磨机有三个设置变量：Y1上砂轮装置角α，Z2上砂轮偏置WO，螺旋沟槽和砂轮的垂直轴间距A≈W+Rg (Rg是砂轮最大直径)。

       2. 排屑槽设计轮廓建模

       钻头横截面要设计得当侧面被研磨时能够出平行切削刃。钻头排屑槽轮廓分为6部分，如图3所示。
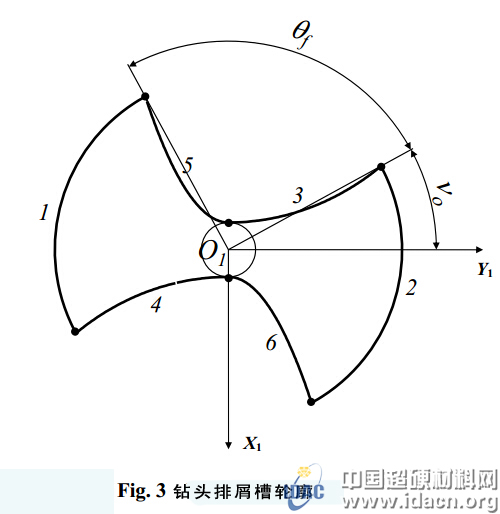
       当钻槽型面设计用连续曲线表示时，钻头排屑槽型面的主切削刃部分由理轮廓线可得，后刀面部分用抛物线表示。由此可以得出钻头轮廓斜面的显式表达式。为求得平行切削，主切削刃型面用连续曲线表示如下：


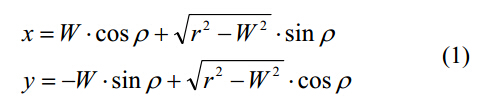
       其中，r是从钻芯厚度W的一半到钻头半径R的变量：


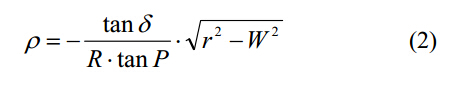
       主切削刃表达式如下：


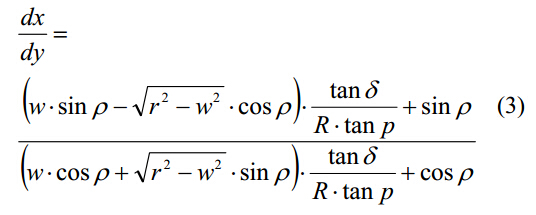
       根据切削刃排屑槽的理论型面，横刃前角表达式如下：


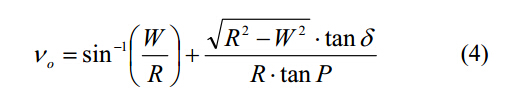
       因此，排屑槽轮廓的在预设坐标系中的定向就可以固定下来。

       后刀面轮廓可以用抛物线表示，表达式如下：


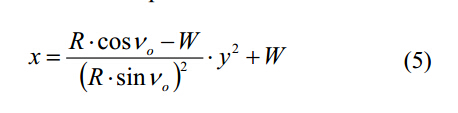
       钻头型面的后刀面斜面表达式如下：


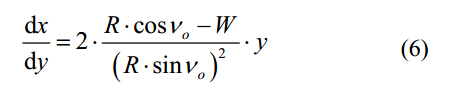
       3. 螺旋排屑槽表面公式

       沿着钻头轴向给排屑槽添加一个螺旋运动，就可以对螺旋排屑槽表面进行建模：


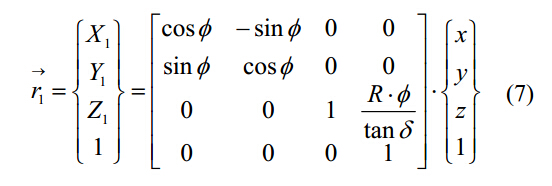
       其中：Φ是钻头螺旋轮廓绕Z1轴的辅助变量，顺着Z1轴方向观察，Φ是顺时针方向的。公式7在钻头轴O1—X1Y1Z1转化为O2—X2Y2Z2时可表达为：


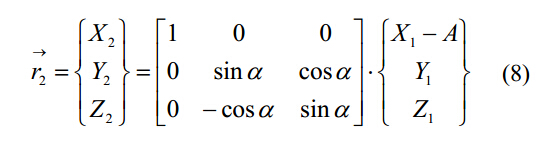
       4. 螺旋排屑槽表面和砂轮间的相切曲线

       螺旋排屑槽表面和砂轮间的相切曲线可以用矢量公式表达如下：


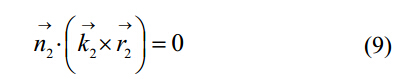
       其中，K2=｛0 0 1｝T是Z2轴的单位向量；n2是螺旋排屑槽表面和砂轮在O2—X2Y2Z2坐标的每一个切点的法向量，表达如下：


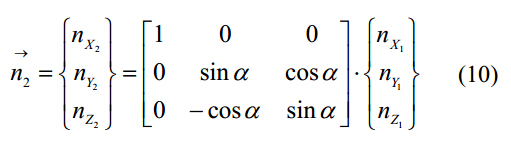
       其中，n1是螺旋排屑槽表面和砂轮在O1—X1Y1Z1坐标的每一个切点的法向量，表达式如下：


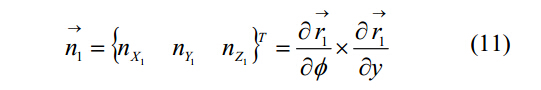
       其中：


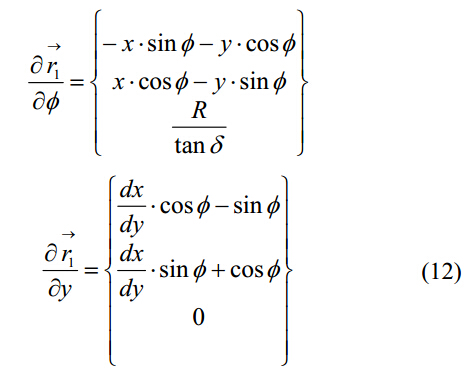
       将式（8）和（10）替换为式（9），相切曲线公式就表达为以下解析式：


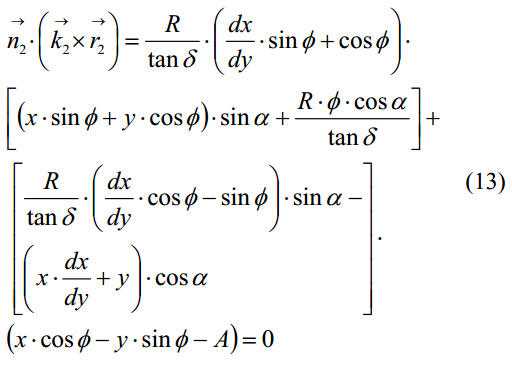
       5. 砂轮轮廓计算

       在求得相切曲线后，将相切曲线绕着砂轮轴旋转即得到砂轮表面；平面上的砂轮轮廓表达式如下：


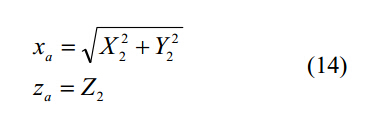
       对于本实验中的自动钻槽研磨机，求得的离散砂轮轮廓通过两条圆弧实现曲线拟合。

       6.砂轮偏置计算

       砂轮偏置WO可以通过图4显示的理论砂轮型面求得。
图4

       理论主切削刃和后刀面在非连续性M上交叉。很显然这样的轮廓型面不太实际可行，不能造出对应的排屑槽设计型面。相反，曲线AMB显示的且在M处有非连续性的砂轮型面就能够满足该条件。此处应注意的是，非连续性M点处的砂轮直径也是砂轮的最大直径Dg。此外，沿着砂轮轴的非连续的位置代表了砂轮偏置WO。

       实验结果

       本研究利用MATLAB工具建立了砂轮设计CAD模型。图形用户界面（GUI）如图5所示：

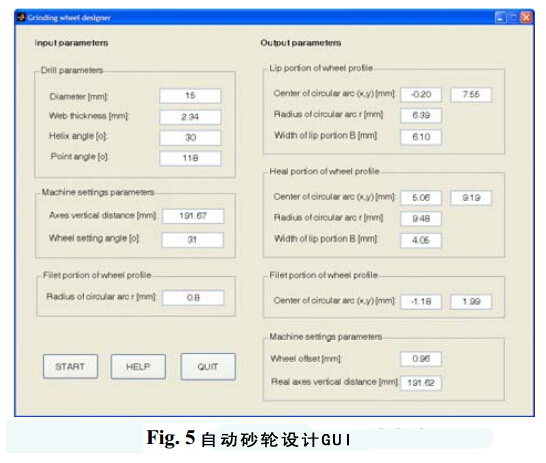
       在砂轮型面设计过程中，用到了钻头直径、螺旋角、顶角、钻芯厚度、砂轮装置角、GUI垂直距离等输入参数。GUI还包括输出参量，如中心坐标、圆弧半径以及图6所显示的砂轮偏置。

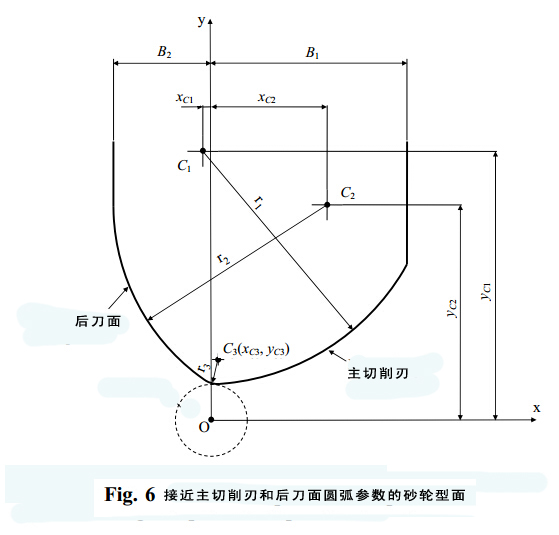
       为求得以下输入参数，图7展示了一个砂轮轮廓：

       D= 15 mm, 2p= 118°, = 30°, 2W= 2.34 mm, A =191.67 mm,α= (30 ÷ 35)°.

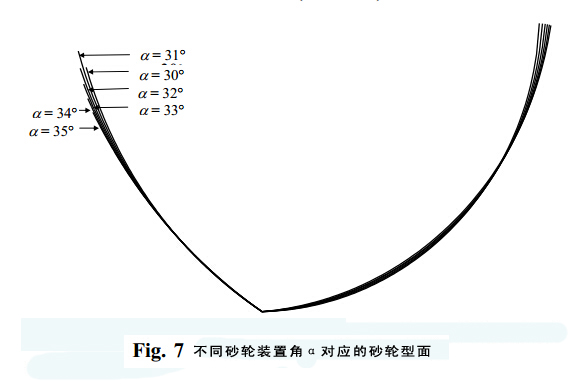
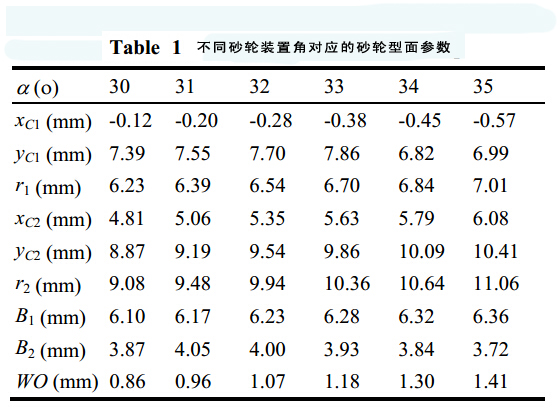
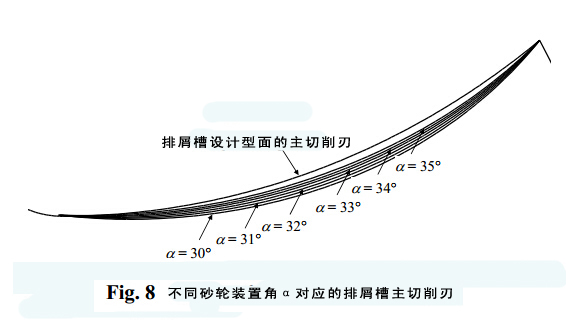
       表1是不同砂轮装置角对应的砂轮轮廓参数值。图8是不同砂轮装置角对应的主切削刃。

       结论

       本研究中的自动砂轮设计程序简化了麻花钻排屑槽生产工艺设计，缩短了选择最佳砂轮几何形状的时间。该CAD模型还可以用来修改其他机器设置变量从而获得排屑槽型面设计的最接近值。