1 砂轮截形的计算
加工汽轮机叶片用叶根铣刀要求精度高、耐磨损且能多次重复使用。该铣刀齿形的轴向截形如图1所示。图中A2B及IJ两段直线垂直于X轴,若采用普通铲磨法加工刀具齿形,则在该两段直线处不能形成侧后角,刀具用于切削时将首先在此处磨钝,即产生“勒刀”现象。若采用分段铲磨方法,即先铲磨A2B和IJ段之外的曲线,再斜向铲磨这两段直线,虽可保证前刃面齿形,但在重磨后齿形将发生改变,影响零件加工精度。若采用整体斜向铲磨法,则HG 直线段的尺寸难以控制。为解决这一问题,在实际生产中可采用修形砂轮辊子对A~G和H~Z两段分别进行斜向铲磨,这种加工方法既可保证刀具重磨后的齿形,又可节省刀具制造工时。

如图2所示,对铣刀进行径向铲磨时,为计算砂轮截形,需已知以下参数:工件截形深度api,被铲磨铣刀外径处端面前角gfa,被铲磨铣刀半径r0,被铲磨铣刀齿形上任一点A的极角di,铣刀截形宽度li,被铲磨铣刀上任一点A处的矢径ri,被铲磨铣刀齿数z0,铲背量K。铣刀轴向截形A点处的坐标为Ti(计算时将各点轴向齿形的纵坐标代入即可),则径向铲磨时砂轮截形的计算公式为ri=r0-Ti
di=arcsin[(r0/ri)singfa]-gfa
对于已给定的工件(铣刀),将各段的轴向齿形坐标代入迭代公式,即可计算出q=0°时的砂轮截形GX(I)和GY(I)。
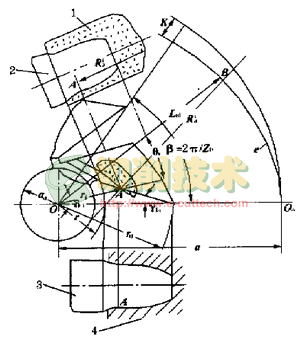
图2 砂轮截形的计算
2 影响砂轮截形的因素分析
斜向铲磨时,砂轮既有铲背运动(阿基米德螺旋运动),又有斜向分运动,此时砂轮截形主要受斜铲角度q、砂轮直径D、工件几何参数等因素的影响。斜铲角度q的影响
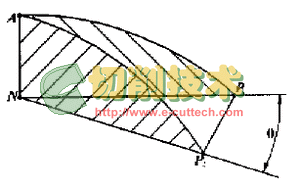
如图3所示,如采用相同的铲背量K,因为NP1=K/tana1,NP2=K/tana2(a1,a2分别为A点处的径向和斜向顶刃后角),又因为NP1=NP2cosq,所以tana2=tana1cosq,即径向和斜向的顶刃后角不同。如径向和斜向顶刃后角相同,即a1=a2,则可得K2=K1/cosq,即K值增大。将切削刃上A点的法向后角记为anA,它与铲磨后角的关系为tananA=tana2sinq。因为tana2=tana1cosq,所以tananA=(1/2)tana1sin2q,即sin2q=2tananA/tana1。
在实际生产中,可根据加工需要选择斜铲角度q值,从而确定当量工件直径D1的值。为保证A2B处良好的切削性能,通常选取anA=3°
砂轮直径D的影响
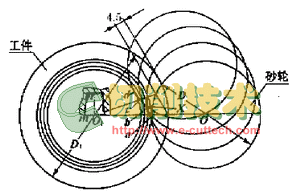
如图4所示,设X为下一个刀齿的顶点,则斜向铲磨时要求当砂轮直径上的点尚未到达或刚好到达X点时,凸轮必须回程,否则将会破坏下一个刀齿的轴向截形。根据砂轮结构特点可知,砂轮最小直径的最大值应为Ø75mm,由此可推断出铲背量K值约为2,将D1及K=2代入迭代公式,并重新计算齿形坐标点,即可得到砂轮的实际截形。
另外,由于对刀不可能十分准确,因此应考虑铲磨时砂轮串位的需要。为此,应对砂轮辊子相应段的尺寸作相应调整。


 手机资讯
手机资讯 官方微信
官方微信








 豫公网安备41019702003604号
豫公网安备41019702003604号