磨料磨具网

       作者：黄云1,2，桂林1，秦涛3，王文玺1,2，邹莱1,2，李恒1†

       作者单位：1. 重庆大学 机械与运载工程学院，重庆 400044；2. 高端装备机械传动全国重点实验室，重庆 400044；3. 中国航发南京轻型航空动力有限公司，江苏 南京 211100

       收稿日期：2023-11-01

       基金项目：重庆市自然科学基金创新群体项目（CSTC2019JCYJ-CXTTX0003），Innovation Group Science Fund of Chongqing Natural Sci⁃ence Foundation（CSTC2019JCYJ-CXTTX0003）；中央高校基本科研业务费专项资金资助项目（2023CDJXY-022），Fundamental Research Funds for the Central Universities（2023CDJXY-022）；重庆市研究生科研创新项目（CYB23021），Chongqing Graduate Research Innovation Project （CYB23021）

       作者简介：黄云（1962―），男，重庆万州人，重庆大学教授，博士生导师

       通信联系人，E-mail：Heng.Li@cqu.edu.cn

       摘要

       本文提出了一种面向叶片前缘廓形精准控制的机器人砂带磨削加工方法. 以轴流压气机叶片为研究对象，结合半赫兹接触理论和有限元仿真获取了柔性磨具和叶片前缘的接触区域内的应力分布，基于Preston方程求解材料去除函数. 遍历刀位点对控制点的磨削深度，建立全局材料去除矩阵，搭建驻留时间求解非线性方程组. 采用带有阻尼因子的Tikhonov正则化消除大型稀疏病态矩阵对求解精度波动的影响，将所求驻留时间转换为对应刀位点的进给速度，生成机器人加工代码. 磨削试验结果表明，基于驻留时间控制的机器人砂带磨削方法能够实现给定允差范围内叶片前缘廓形的精准加工，型面误差可以控制在0.02 mm以内.

       关键词：压气机；砂带；柔性磨削；前缘廓形；驻留时间

       引言

       航空发动机是飞机的核心部件之一，直接关系到飞机的性能和安全，不仅是国家重点发展领域之一，也是推动国家经济、科技和军事发展的重要引擎之一［1］. 叶片前缘的加工直接决定了叶片的气动性能和服役寿命，然而叶片前缘部分由于曲率变化剧烈、刚性差且弯曲和扭曲程度大，并且使用的钛合金材料导热系数低、弹性模量小，属于典型的难加工部位， 对实现叶片的精密磨削带来了极大的挑战［2-5］.

       砂带磨削是一种柔性加工方法，兼具磨削和抛光功能 . 它具有高效切割、冷态磨削、灵活工艺性和广泛适应性等诸多优点 . 因此砂带磨削被广泛用于精密磨削加工复杂自由曲面，尤其在叶片加工中发挥着重要作用. 它是提高叶片型面精度、表面完整性和加工一致性的有效方法之一 . 面对余量分布不均的叶片加工，需要精确的材料去除函数来开展工艺参与规划，众多学者对此做出了大量的研究 . Guo等［6］针对叶片前尾缘的多余材料去除问题提出通过构建临时引导模型来指导加工过程 . Wan 等［7］利用公差带来提高叶片定位能力以避免叶片出现过磨 .Wang 等［8］采用非接触式冷加工方法，针对叶片前缘难加工问题进行了电解加工叶片边缘的尝试，通过阴极的刀具沿叶片平均弧度线切向进给，对叶片前、后缘进行电化学加工 . Mu等［9］在叶片加工稳定性方面进行研究，通过机器人七轴联动砂带磨削系统的区域力控来实现加工过程中接触力的实时控制并减少每个区域的力信号波动 . Sarma 等［10］针对数控磨削加工道路轨迹生成进行了研究，提出了一种综合考虑制造与测量的轨迹生成方法.

       当前学者针对压气机叶片边缘的精准去除已经开展了全面而深入的研究，揭示了加工工艺参数与材料去除之间的紧密联系 . 但是由于过去的研究都是逐点调控，无法解决砂带柔性磨削接触面积大、刀位点之间干涉严重的现象，而计算机控制光学表面形成中常用的驻留时间控制加工方法，作为一种全局求解的方法能很好地解决这类问题. 因此，本文根据 Abaqus仿真分析获得接触区域的应力分布，代入半赫兹接触中并对结果进行修正，通过 Preston 方程建立对应区域的去除函数模型；基于全局求解的思想，在叶片表面引入控制点和驻留点，通过遍历驻留点和控制点的方式获取砂带柔性磨削的加工轨迹，考虑了加工时对相邻刀位点的影响，更符合砂带柔性磨削加工的特点.

       1叶片前缘去除函数建模

       1.1 Abaqus接触状态有限元仿真

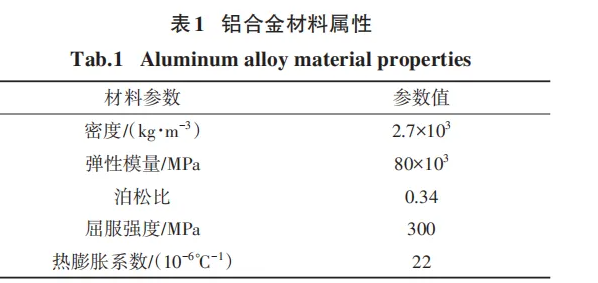
       利用有限元仿真软件 Abaqus 对叶片前缘和柔性磨具进行接触状态的仿真研究 . 首先将叶片的三维模型导入 Abaqus，叶片模型材料为铝合金，采用Johnson-Cook（JC）本构损伤模型［11］模拟加工叶片时材料的失效状态. 铝合金材料属性如表1所示.

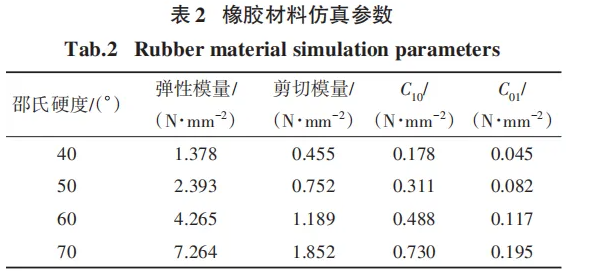
       考虑到有效接触区域以及减小仿真试验的计算压力，接触轮模型只取了 5% 区域，柔性磨具的材料采用制备接触轮的丁腈橡胶 . 橡胶材料仿真参数如表 2所示，橡胶材料属于超弹性材料，且本次仿真试验属于小变形的加工范围，故采用橡胶材料常用的Mooney-Rivlin应力-应变本构模型［12］表示.     

       式中：H为超弹性材料橡胶的应变能密度；T1、T2表示变形张量不变量；C10、C01表示橡胶材料硬度有关的材料弹性系数.

       根据实际加工需求，对叶片施加了榫头部分的单端固定约束，接触轮沿叶片边缘施加垂直于叶片的法向力，网格采用的是以六面体为主的C3D8过渡网格，中间加密处的网格单元尺寸为 0.2，通过观察接触部分的应力变化并对其进行分析，该模型能够准确反映材料在高应变速率下的变形行为，进而为后续研究中建立材料去除模型提供接触区域的应力分布.

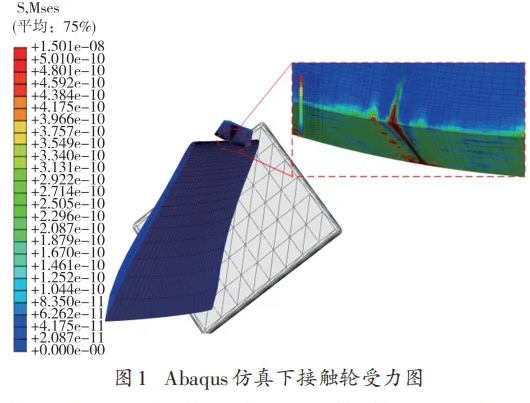
       由于砂带相对于接触轮厚度很薄并且产生的变形不明显，在分析接触部分的应力变化中影响很小，因此在 Abaqus 中做了简化处理 . 当下压量为 3 mm时，Abaqus仿真下接触轮受力图如图1所示，接触轮与前缘接触后发生了非线性弹性变形，在接触区域形成应力集中，接触区域两侧的应力随着距离接触中心增大而减小 . 接触轮不同截面的应力分布曲线如图2所示，等效应力状态云图近似于正态分布.

       1.2 建立叶片前缘材料去除模型

       Preston方程是被广泛应用并被证实具有很高可信度的经验公式. 此方程是由Preston［13］在1927年提出的，即

       式中：dz/dt表示刀位点单位时间内的去除量；k 为比例系数，由除了接触压力p和瞬时相对速度v以外的影响因素共同决定，如磨料类型、工件材料等 . 根据Preston方程可以推导出在加工点（x，y）处停留时间T对应的材料去除量：

       根据式（2）可推出对应叶片边缘上任一点的去除函数为：

       式中：H（x，y）表示在设定刀位点处的材料去除率.在实际叶片前缘加工过程中，在多种不同的接触状态 接触轮与工件存，如图 3和图4 所示 . 图 3 中R0为接触轮半径，l0为橡胶轮宽度，d0为接触区域的弹性变形高度，Fn表示加工叶片的轴向力，Ft表示工件受到的接触反力. 根据赫兹接触理论［14］，当两个物体接触并压紧时，初始接触点附近的材料会发生局部变形. 弹性接触理论基于以下假设：①接触物体只产生弹性变形，并符合胡克定律；②接触力垂直于接触面；③接触面的尺寸远小于接触物体表面.

       在接触轮与叶片的接触中，边缘处的材料去除量较小，接触轮始终保持弹性接触状态. 在砂带磨削过程中，当砂带绕回转中心O点匀速转动时，可以将砂带和接触轮视为一个完整的整体，接触轮与前缘之间存在方向接触力，前两个条件符合赫兹接触理论，由于叶片前缘部分曲率变化大，本文采用半赫兹接触理论求解接触应力分布模型.

       半赫兹接触是由Ayasse等［15］在赫兹接触的基础上提出的运用于曲率变化大时的求解方法，即在曲率变化小的方向仍然引用赫兹接触理论，而在接区域曲率变化大的方向上不再采用赫兹接触理论，其基于接触轮与叶片前缘的虚拟穿透来对接触区域进行快速确定. Ma等［16］假设车轮和钢轨不发生弹性变形，采用半赫兹接触的虚拟穿透法测定了轮轨接触区域的接触斑块并建立了对应的轮轨接触模型 .半赫兹接触可以有效地解决某些赫兹接触不适用的情况，如图 5 和图 6 所示，接触轮与叶片前缘廓形接触时，其曲率不断发生变化，因此使用半赫兹接触理论对于解决本文研究的砂带磨削叶片前缘问题具有充足的合理性.

       接触轮加工叶片前缘时，半赫兹接触示意图如图 7 所示，在接触区域内沿着叶片曲率变化方向将其划分为 n 个条带，带宽为 Δx，拥有最大高度 H0的条带称为母带，对应的长、短轴曲率分别为 A0、B0，半轴长a和b分别为：

       式中：n为椭圆半轴系数；r为弹性趋近量；E*为等效弹性模量；ai为每一个条带处的曲率所对应的长半轴；δi为每一个条带处的曲率所对应的干涉深度；ε为修正系数（针对x轴方向曲率不变）.

       通过 Abaqus 有限元仿真中接触区域的应力分布，结合课题组自行开发的 CAM 软件离散待加工叶片的前缘部分，提取加工路径点 u、v向的曲率 . 根据前缘的曲面特征，沿着叶片边缘方向（u向）的曲率可近似看作不变，提取曲率变化大的方向（v向）的曲率值，代入式       （4）和式（5）即可求得叶片前缘的应力分布值，进而通过边缘处应力分布求解该区域的材料去除深度.

       2驻留时间预规划

       2.1 搭建叶片前缘全局材料去除矩阵

       在第 1 节中，建立了一个叶片前缘部分的材料去除模型，该模型采用修正的 Preston 方程并结合Abaqus有限元仿真 . 本节将针对叶片前缘曲率变化大和难加工的特点，通过轨迹规划的方法来实现对前缘廓形的加工.首先对于曲面复杂的前缘廓形，通过对比蓝光扫描的待加工叶片前缘点云模型和理论数模获取叶片前缘的加工余量 . 为了解决砂带柔性磨削接触面积大和刀位点之间干涉严重的问题，本文提出在叶片待加工表面上引入控制点和驻留点，每个控制点对应着待加工表面上相应点的余量，而驻留点则是机器人砂带磨削时走刀的点位，通过遍历驻留点和控制点的方式，以精准去除控制点对应余量为目标进行基于驻留时间的轨迹规划 . 这一轨迹规划过程可以用对应的矩阵形式表示：

       式中：R为去除函数矩阵，Rm，n表示的是接触轮在第n个驻留点时对第m个控制点的去除量；t为驻留时间矩阵；b为残余误差矩阵.

       航空发动机叶片加工的要求是将待加工叶片与理论廓形之间的残余误差 E 控制在公差范围内 . 利用驻留时间去除叶片边缘余量的原理是将待加工叶片与理论廓形之间的残余误差 E 作为目标函数，去除函数的第n行R（n，：）表示叶片边缘所有驻留点对第n个控制点的去除能力 . 将 R（n，：）与对应的 tn相乘，可以得到叶片所有驻留点对第 n 个控制点的去除总量. 相对于常规加工方法，这种方法的优势在于它不仅考虑了接触点处的材料去除，还考虑了对磨削范围内其他控制点的去除能力. 此外，通过调整驻留点的疏密程度，合实际工程应用 可以控制加工表面的精度，使其更加符合实际工程应用.

       获取去除函数矩阵 R 前，由于叶片边缘曲率变化大，并不像平面一样可以直接判断控制点是否位于驻留点的接触范围之内，需要对此作出适当的处理. 加工路径上的接触判断图如图8所示.本文以任一驻留点为原点，求出当前驻留点的切平面和法矢，以指向下一个驻留点的方向为x轴，法矢和x方向的叉乘作为y轴，建立一个新的局部坐标系.在新的坐标系下以x、y轴作为投影平面将所有控制点投影到该平面上，再通过式（8）的坐标变换矩阵G得到所有控制点在局部坐标系下的坐标.

       式中：（xc，yc，zc）表示驻留点在世界坐标系下的三坐标；（xx，yx，zx）、（xy，yy，zy）和（xz，yz，zz）分别表示局部坐标系下的 X、Y、Z 坐标轴在实际坐标系下的三坐标形式.率法矢夹角小于 控制点在局部坐标系 X 方向的坐标（筛选主曲90°的坐标）如图9所示.

       本文引入筛选矩阵Q，它由法矢筛选矩阵QA和椭圆接触筛选矩阵QB组成.由于叶片前缘的曲率变化很大，如果仅按照投影到局部坐标系下的坐标进行椭圆接触判定，会导致一些控制点无法被正确判定为接触到.

       因此，根据实际加工情况设置了一个判定控制点和驻留点之间法矢夹角的条件；然后，通过椭圆接触筛选矩阵 QB进行二次筛选，并将筛选后的投影坐标代入先前求得的材料去除模型中，得到一行的去除函数矩阵. 通过对每一个驻留点进行遍历，最终可以得到去除函数矩阵R.

       2.2 驻留时间的求解

       R（m，n）矩阵的每一列表示的是路径上砂带在每一个驻留点时对该控制点的单位时间材料去除率. 为了保证加工精度，控制点的数量一般是远远大于驻留点的数量，并且由于接触轮的接触区域相对于工件较小，去除函数矩阵 R 是一个大型的稀疏矩阵. 由于该稀疏矩阵往往是个病态矩阵，向量行数m远大于列数 n，因此无法获取精确解，众多学者从奇异值分解、最小二乘正交分解法（Least Squares QR-Factorization Method，LSQR）、二次规划寻优等多种角度进行研究和优化，在实际应用中，加工前缘并非需要精确解，大多数情况下，   LSQR 和 Tikhonov 正则化下的解即可满足加工要求.

       大型稀疏矩阵往往是病态矩阵，LSQR算法并不是直接求出最优解 x，而是遵守最小二乘原则，在限定的空间中寻找最优解. 主要为求解式（9）的线性方程组，且保证其二阶残差范数最小. 

       Tikhonov 正则化则是从提高解的稳定性和减少驻留总时间的角度出发，对去除函数矩阵 R 进行正则化处理，以优化驻留时间 t. 在去除函数矩阵 R 中引入一个数量阵T，数量阵T引入的阻尼因子w表示驻留点密度与表面误差间的权重关系，理论上 w 的取值区间为［0，+∞），但w的值越小，取得非负驻留时间的可能性越小；而当w的值越大时，加工后的表面误差也就越大. 矩阵如式（10）所示

       数量阵 T 将去除函数矩阵 R 由 m 行 n 列扩展为（m+n）行n列的矩阵RW，同时将加工余量列向量b补充 0 以 扩 充 成（m+n）维，基 于 式（6）和 改 进 后 的式（11），将最小二乘问题转换成亏秩矩阵的求解问题.

       合理地选择阻尼因子 w 的值，以保证叶片前缘廓形高精度的同时，符合实际加工特点是 Tikhonov正则化的关键所在. 去除函数矩阵R如图10所示.

       2.3 仿真验证

       为了确定基于驻留时间加工叶片前缘的可能性和寻找合适的阻尼因子w，本文以最终型面误差E和驻留总时间 Tsum为优化方向设计了 Tikhonov 正则化的仿真试验 . 叶片前缘驻留点和控制点示意图如图11所示.

       由图 11 可知，在叶片前缘处提取 300 个驻留点（红色点集）和 1 600 个控制点（绿色点集）作为本次仿真试验的对象 . 本文通过反复迭代调整 Tikhonov正则化中阻尼因子 w 的值，最终选定 w 取 0.4 时最佳 . 图 12对比了未加工的叶片前缘（Origin）在 LSQR算法和Tikhonov正则化下的最终型面误差E.由图12可以明显看出，2种算法下叶片前缘的加工余量都有所减小，相比较而言，LSQR 算法的去除率在全控制点下约为64.6%，Tikhonov正则化的去除率在全控制点下约为93.6%，因此采用Tikhonov正则化算法下叶片前缘处的型面误差 E 有着显著减小，并且叶型趋近于理论廓形.

       3实验验证

       第2节通过 MATLAB 的仿真试验证明了优化叶片前缘廓形的可行性，本节通过实验验证基于驻留时间的前缘轨迹规划在砂带磨削加工中的有效性.

       本实验采用的是如图 13 所示的团队自行搭建的机器人砂带磨削平台，该系统主要由工业机器人、橡胶接触轮、砂带、力传感器和ACF恒力浮动装置组成 . 采用 Fanuc 工业机器人（M-710IC/50）作为运动载体夹持叶片，磨削力由磨具端的 ACF 恒力浮动打磨装置（精度 0.1 N）控制，磨削实验使用 3M 公司生产的粒度为A6（P2000）的237AA金字塔堆积磨料砂带，线速度为 10 m/s，法向磨削力为 5 N. 根据驻留时间 ti，j和两个驻留点间的步长 hi-1j和 hi，j可以计算出Fanuc机器人的进给速度vi，j，如式（12）所示.

       图 14（a）为未加工的叶片实物图，图 14（b）为基于驻留时间调控的对前缘5%~95%叶高处进行磨削加工后的叶片.

        通过对比磨削前、后的叶片前缘廓形，可以明显看出磨削后的叶片边缘更加光顺，表面粗糙度也有了显著降低. 采用GOM三维蓝光扫描仪对磨削后叶片进行检测，将采集到的点云模型与理论模型进行比对. 图15为磨削后前缘不同截面轮廓线和尺寸偏差，分别提取了叶高的30%、50%和70%叶片处截面廓形，截面包含了理论廓形（光滑彩色线条）与其加工的公差带（棕色区域），不规则曲线段为前缘的实际加工廓形，两曲线间的差值表示实际加工廓形与理论廓形之间的差距 . 由图 15 可以看出，叶片前缘廓形误差相较于未加工之前有了明显的减小，前缘廓形线基本处于+0.03~-0.05 mm 的公差带之间，与理论廓形之间的型面误差E在0.02 mm以内.

       4结论

       本文针对压气机叶片前缘柔性磨削接触状态不明，廓形精度难控制的问题，制的砂带磨削方法 提出了基于驻留时间控，具体的研究结论如下：

       1）考虑叶片边缘狭窄区域内曲率急变的特征，将半赫兹接触理论引入柔性磨具和叶片边缘的接触问题求解，初步求解了接触区域内的应力分布，通过Abaqus有限元仿真对接触部分的应力分布曲线进行了验证和修正，基于获取的应力分布和 Preston 方程建立了叶片前缘的材料去除模型.

       2）基于材料去除模型，遍历控制点搭建了全局材料去除模型矩阵，建立了驻留时间求解线性方程组. 以加工余量最小化作为目标函数，引入带有阻尼因子的 Tikhonov 正则化，求解驻留时间分布并转化为进给速度，仿真表明余量有效去除达到93.6%.

       3）在课题组自行搭建的机器人砂带磨削平台上开展了叶片前缘磨削实验，结果表明，磨削后的叶片前缘轮廓线基本在+0.03~-0.05 mm 的公差带之间，与理论模型之间的型面误差E在0.02 mm以内，证明了本文所提方法能够实现叶片前缘的精准加工.