磨料磨具网

摘要　基于一种利用热管技术对磨削弧区进行强化换热的构想，采用FLUENT软件建立了环形热管砂轮干磨削温度场的仿真模型，得到了热管换热能力与热流密度、转速和砂轮壁厚的关系，并在相同热流密度下对比了热管砂轮与热管砂轮弧区的温度。仿真结果表明：弧区温度会随着密度的增大相应升高，温度明显低于无热管砂轮。最后通过干磨削钛合金TC4试验，对仿真结果进行了验证。

关键词　热管砂轮；温度场；Fluent软件；干磨削

　　在难加工材料的磨削中，研究磨削温度场对控制弧区温度有很重要的意义。计算机住址技术作为辅助工具广泛应用于磨削温度场的研究，它既可以研究各种材料高质量加工的磨削工艺，也可以对磨削温度、磨削力等进行预测，因此，越来越受到工程领域人们的关注。

　　本文根据一种利用热管强化弧区热管强化区换热的创新构想，将采用计算机仿真技术，建立热管砂轮干磨削温度场的有限元模型，利用Fluent仿真软件进行数值模拟，验证利用热管技术强化磨削弧区换热的创新构想，研究砂轮内部的热管结构能否最大限度地疏导出已产生的积聚在弧区的磨削热，有效抑制磨削烧伤和进一步提高磨削效率；分析在不同热流密度、转速和壁厚参数下，热管温度场随热流密度变化规律，并与无热管砂轮进行对比。结合仿真与试验结果指导工艺参数的选择，进一步挖掘热管砂轮的换热潜力和应用前景。

1         热管砂轮仿真几何模型的建立

1.1       几何模型

根据砂轮盘形结构，采用回转型热管形式置于砂轮中。如图1所示，当砂轮旋转起来，工质在离心力的作用下均布在整个外圆内壁上，形成厚度为δ液膜；弧区的热量q也近似均匀分布于整个砂轮的外圆面上，此处视为热管的蒸发端，换热面积为为内壁面积Ａ。在砂轮两端面靠近内环处有一圈圆周环槽，此处视为热管的冷凝端。热量从磨粒经外圆面通过砂轮壁面传入内腔时，工质开始吸热，当液膜的温度达到沸点时汽化，蒸汽会在压差的作用下向冷凝端移动，并在冷凝端进行热量交换发生液化；内部工质的回流是利用自身旋转产生离心力而驱动的，只要有足够的旋转速度，就能保证工质的回流。

图1　环形热管内腔换热原理示意图

　　仿真模型包括砂轮基体、热管结构、磨粒和热源部分。热管砂轮基体采用圆环二维平面模型，圆环大径与砂轮直径相同为Φ320mm，圆环小径与圆环槽即冷凝端的尺寸相同为Φ240mm。从图1的局部放大图可经看到，圆环外分布一圈有序排布的金刚石磨粒，工件简化成一道热源并输入一定的热流密度。

　　采用专用的前处理软件GAMBIT进行建模和网格划分工作，为获得较高的计算精度和效率，将尺寸较小的磨粒和尺寸较大的砂轮基体采用逐渐过渡的方法划分为三角形非结构网格。近热源处局部模型及网格划分见图2所示，所建型共737714个网格单元。

　　网格质量对计算精度和稳定性有很大影响，因此，为了保证计算的精度同时兼顾计算效率，需要对网格质量进行检查。本文针对实际的模型，为了得到较好的网格质量，提高计算精度，采用分区分别划分网格的办法。网格类型主要为三角形网格，95%的网格Q_EAS值小于0.5，网格质量好。

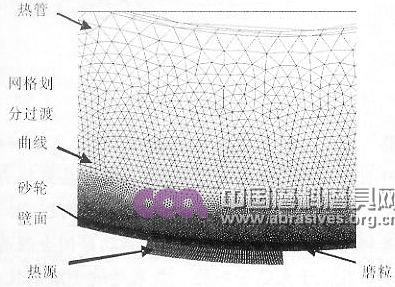
图2　热管砂轮近热源局部网格模型

1.2      边界条件

　　参考压强设为101325Pa，环境气体温度为300K，热流密度的输入边界热管冷端边界设为壁面边界条件，砂轮运动类型设置为Moving Reference Frame。

1.3      材料物性值

　　一般情况下，热管砂轮启动后导热率是铜的100~1000倍，定义砂轮内腔的热管结构其导热系数为铜导热系数的100倍，即3900W/(m·K)。磨料层包括金刚石与结合剂，根据两者所占面积的面分数可以计算得到磨料层的平均导热率为138 W/(m·K)。同时砂轮的壁面材料也需要定义密度、比热和导热系数。各种材料的属性见下表1。

　　　表1　各种材料的属性

2         数值计算结果与分析

　　利用计算流体力学软件Fluent2DD求解器对热管砂轮干磨削温度场进行了数值模拟。建立求解模型时选择非耦合求解法的隐式算法，其他为默认选择；然后选择标准K-e模型求解方程，选中其中的能量方程。以上设置完成后，设置边界条件，最后初始化流畅进行迭代求解。

2.1      弧区温度的影响因素

2.1.1       热流密度对弧区温度的影响

　　热流密度可以用来表征磨削弧区热量的大小，施加的热流密度大小为20Wmm²，热管砂轮转速为3000r/min，壁厚为1mm，冷却壁面温度为300K。在Fluent软件中选择稳态求解器，当弧区温度平衡时，管砂轮温度场如图3所示。

　　为了挖掘热管砂轮的换热能力，分别设置不同的热流密度20W/mm²、40W/mm²、60 W/mm²、80 W/mm²，得到弧区温度随热流密度变化的曲线，如图4所示，从图中可以看出，热管砂轮弧区温度随热流密度呈线性变化，随热流密度的增大弧区温度升高。当热流密度为20W/mm²时，弧区的平衡温度341K；当热流密度达到80W/mm²时，弧区温度也只有463K。因此，热管砂轮的弧区温度随热流密度的增大呈线性升高，且在热流密度80W/mm²时，也能控制弧区温度在500K以下。

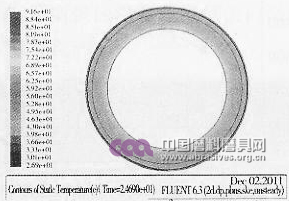
图3　热流密度20W/mm²时热管砂轮温度场

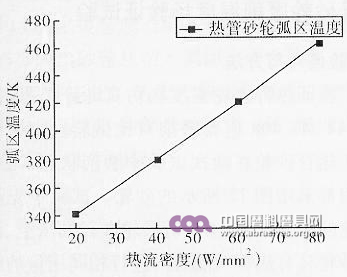
图4　弧区温度随热流密度的变化规律 

2.1.2       转速对弧区温度的影响

　　设置砂轮转速8000r/min，壁厚为1mm，施加的热流密度为20 W/mm²，冷端壁面条件为300　Ｋ,在Fluent软件中选择稳态求解器，当弧区温度平衡时，热管砂轮温度场如图5所示。

　　为了探究转速对热管砂轮换热能力的影响，分别设置转速为1000 r/min、3000 r/min、5000 r/min、8000 r/min，得到弧区温度转速变化的曲线，如图6所示。从图6中可以看出，热管砂轮弧区温度随砂轮转速的增大而降低。从传热学的角度看，当转速增大，热量更加均匀地分配在整个砂轮外壁上，使换热更加均匀，而不会集中在弧区，所以温度会随着转速的增大而降低，且当转速在3000 r/min以下时，弧区温度随转速变化较明显，与1000 r/min的温差达28K；而在3000 r/min以上，弧区温度变化仅2~8K，变化趋势较缓慢。

图5　砂轮转速为8000r/min时热管砂轮温度场

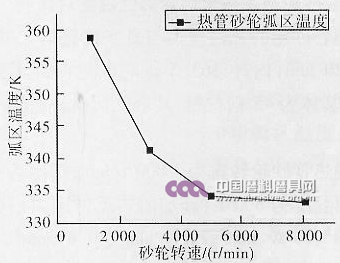
图6　弧区温度随砂轮转速的变化规律

2.1.3       壁厚对弧区温度的影响

　　设置热管砂轮壁厚1.5mm，转速3000 r/min，施加的热流密度20 W/mm²，冷端壁面300K，在Fluent软件中选择非稳态求解器，弧区温度变化曲线如图7所示，热管的启动时间即弧区温度开始保持不变的点所对应的时间坐标为16s。

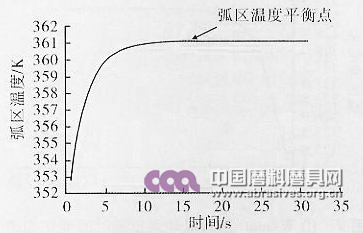
图7　弧区温度随时间的变化规律 

　　为了探究砂轮壁厚对热管砂轮换热能力的影响，分别设置壁厚为0.5mm、1 mm、1.5 mm，得到启动时间随壁厚大小变化规律，如图8所示，从图8中可以看出，热管砂轮的启动时间随壁厚的增加而变长，这一结果对热管砂轮的设计有一定的指导意义，减小砂轮外壁厚度可以加快热管砂轮的启动时间。同时也得到，砂轮壁厚在0.5~1.5 mm范围内，弧区温度变化并不大。

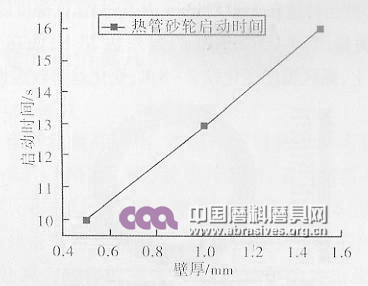
图8　启动时间随壁厚的变化规律

2.2      热管砂轮与无热管砂轮弧区温度对比

　　无热管砂轮的几何模型与真实砂轮的尺寸相同，外径Φ320 mm，内径Φ63.5mm，砂轮内部无热管结构，整个基体为45钢材料，其余几何条件与热管砂轮相同。

　　设置热管转速为3000 r/min，壁厚为1mm，冷端壁面温度为300K，施加的热流密度大小分别为10 W/mm²、15 W/mm²、20 W/mm²、40 W/mm²，与无热管砂轮在相同转速、相同热流密度下的弧区温度对比，在Fluent软件中选择一阶非稳态求解器，热管砂轮与无热管砂轮弧区温度随时间变化规律如图9、图10所示。从图中可以看出，热管砂轮弧区温度在8s之前弧区温度上升由急到缓，8s之后缓慢趋于平衡；而无热管砂轮弧区温度呈直线上升，30s时已经达到540K。

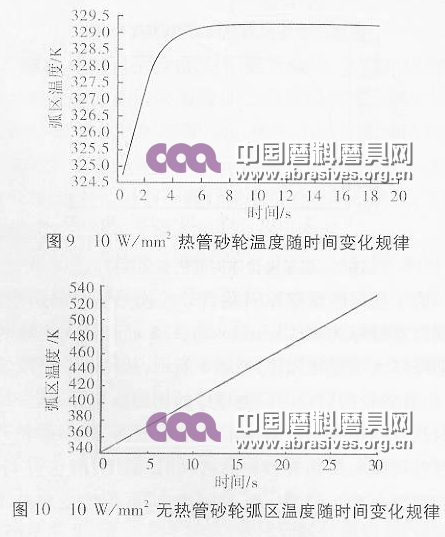
　　为了探索热管砂轮的换热优势，分别在不同热流密度下对比热管砂轮与无热管砂轮弧区温度，结果如图11所示。从图11中可以看出，在同一热流密度下，热管砂轮弧区温度明显低于无热管的普通砂轮，且随热流密度增大热管砂轮的换热优势更加明显。在30s时，热管砂轮早已达到平衡温度，而无热管的普通砂轮温度仍处于上升趋势，而且热流密度较大如40 W/mm²时热管砂轮弧区的平衡温度仅381Ｋ，而无热管的普通砂轮弧区温度为1310Ｋ，两者相差900Ｋ左右。

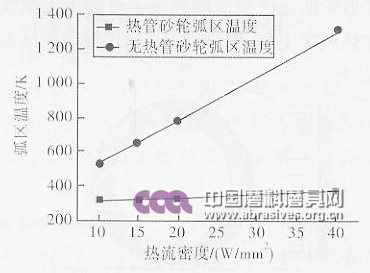
图11　热管砂轮与无热管砂轮弧区温度对比

3         热管砂轮磨削温度场验证试验

3.1      试验条件与方法

　　为了验证热管砂轮温度场仿真计算结果，在磨床PROFIMAT MT408进行磨削对比试验。为保证热管砂轮与无热管砂轮在再次试验中磨削状态一致，整个试验过程都采用图12所示的砂轮。试验中先进行无热管砂轮的磨削试验，然后对砂轮进行抽真空、注液与封尾使砂轮具有热管功能后再进行相同用量的磨削试验。

图12　电镀有序排布金刚石磨粒的热管砂轮图

　　试验测温采用分块试件夹丝半人工热电偶测量弧区工件表面温度分布，试件材料选用钛合金，具体试验条件见表2。测得磨削弧区前后工件表面的最高电势，根据钛合金－康铜丝与标准热电偶标定曲线即可换算出所对应的弧区温度。试验测力选用KISTLER三相压电晶体测力仪。

表2　热管砂轮磨削验证参数

3.2      试验结果与分析

　　图13所示为电镀金刚石热管砂轮磨削钛合金热电热原始信号，从图中可以看出，进入磨削弧区后，温度曲线出现密集排列的尖脉冲信号，这是磨粒磨削点温度的反映，磨削弧区温度是测量值内络线的最高点的值乘以标定值。

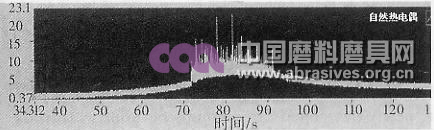
图13　电镀金刚石热管砂轮磨削钛合金热电势原始信号

　　图14为电镀金刚石砂轮磨削钛合金的原始信号，可以反映出砂轮从切入到切出整个磨削过程，力信号呈现周期性变化。从放大的力信号（图15）可以看出，砂轮只有近1/3的部分接触到工件，切向力取最集中的一段信号的平均值。

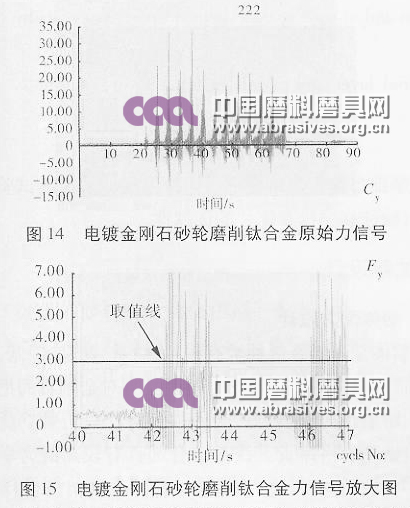
　　为了与仿真的磨削温度相比较，磨削弧区产生的热流密度可以通过公式1计算得出：

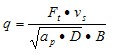　　　　                         （1）

　　其中， －切削深度，mm；

　　D－砂轮直径，mm；

　　B－磨削宽度,mm；

　　Ｆ1－磨削切向力，Ｎ；

　　v_s－砂轮线速度，m/s。

　　结合试验数据和仿真数据，做出热管砂轮与无热管砂轮弧区的对比结果，如图16所示。从图16中可以看出试验和仿真证明了热管砂轮的弧区温度明显低于无热管的普通砂轮。试验中当热流密度达到22时，无热管砂轮的弧区温度近似达到973K，工件表面已经烧伤；而热管砂轮弧区温度仅为663K，降低了近50%，且当切深增加0.05mm时，弧区温度为773K，温度上升的速率降低。由此可见，试验结果与仿真结果趋势一致，热管砂轮在磨削过程中能够实现弧区的强化换热，并降低磨削温度。

　　另一方面，在相同热流密度下，试验结果比仿真结果偏高，其原因主要是在建立仿真模型时认为热管砂轮始终处于理想的良好工作状态，然而在实际磨削试验中，热管砂轮的换热能力会受到热管结构、砂轮转速以及冷端散热条件等因素的影响，所以试验中热管砂轮不能达到与仿真相同的理想工作状态，造成了试验结果比仿真结果偏高。

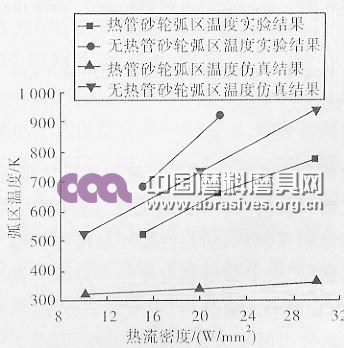
　图16　干磨削钛合金对比验证试验结果

4         结论

　　（1） 从热管仿真研究结果可以看出，弧区与热流密度和砂轮转速等参数相关，热管砂轮弧区温度随着热流密度增大而升高，在热流密度80 W/mm²时，也能控制弧区温度在500Ｋ以下；随着砂轮转速的增大，磨削弧区温度会降低，从仿真结果看，转速在3000 r/min以下，弧区温度变化较快，3000 r/min以上，弧区温度变化缓慢；外壁厚度主要是对热管砂轮的启动时间有影响，壁厚为0.5mm时，启动时间仅10s。

　　（2） 通过仿真和试验结合，对比结果表明，热管砂轮热弧区温度明显低于无热管砂轮，而且随着热流密度的增大，热管砂轮的换热优势不断增大，两者温差越来越大。从仿真结果看，热流密度10 W/mm²时，热管砂轮弧区321Ｋ，比无热管砂轮温度低近200Ｋ；在热流密度为30 W/mm²时，二者弧区温度相差近550Ｋ。从试验结果看，在砂轮切削尝试单因素试验中，砂轮线速度为50m/s，工件进给速度60mm/min，当切削深度0.15mm时，其磨削温度相对于无热管砂轮降低了近50%，且随着磨削用量的增加，二者的温度相差越大，换热能力变强，换热优势更加明显。

参考文献：

[1]　傅玉灿，孙方宏。徐鸿钧，等.缓进给断续磨削时射流冲击强化磨削弧区换热的实验研究[Ｊ].南京航空航天大学学报，199，4（2）：152－155.

[2]　于勇.Fluent入门与进阶教程[Ｍ].北京理工大学出版社，2010.

[3]　JUDD R L,AFTAB K,ELBESTAWI M A.Investigation of the use of heat pipes for machine tool spindle bearing cooling.International Journal of Machine Tools&Manufacture,1994,34:1031-1042.

[4] JEN T C,GUTIERREZ G,EAPEN S,et al.Investigation of heat pipecooling in drilling applications.Part I:preliminary numeriacl analysis and verification[J].International Journal of Machine Tools&Manu-facture,2002,42:643-652.

[5]　李莉，齐乐华，杨方，等.液滴喷射过程流畅和温度场的数值模拟[Ｊ].航空党报，2007（3）：719－724.

[6]　JIN T,STEPHENSON D J.Heat flux distribution and convective heat transfer in deep grinding [J].Machine Tools&Manufacture,2006,46:1862-1868.

[7]　杨世铭，陶文铨.传热学[Ｍ].北京：高等教育出版社，2006.

作者简介

梁星慧，女，1987年生，南京航空航天大学机电学院硕士研究生，主要研究方向：高效精密加工技术。