磨料磨具网

摘要：高温合金因其良好的材料性能被广泛的用于各领域，超声振动辅助磨削已经成为磨削镍基高温合金等难加工材料的潜在技术。本文基于椭圆超声振动辅助磨削（EUVG）运动学分析构建了不同工艺下的磨削形貌仿真模型并计算磨削表面粗糙度，探究超声振动幅值对EUVG磨削表面加工质量的影响规律。结果表明EUVG具有独特的磨削表面形貌，能够实现对于表面纹理的细化以及打断效果，并明显的降低磨削表面粗糙度。最后通过单颗粒以及砂带磨削实验验证模型的可靠性。为探索GH4169高温合金EUVG的高质量加工工艺参数优化提供了理论依据。

       1.超声振动辅助砂带磨削表面创成分析

       磨粒沿着磨粒运动轨迹，对工件进行材料去除以及表面形成。二维超声振动辅助砂带磨削相较于一维超声振动辅助磨削的磨粒轨迹明显不同并且对工件材料去除、磨削表面形貌与粗糙度等都造成一定影响，本章对磨粒进行了运动学分析、建立了磨粒以及砂带的数学模型并进行了表面形貌的仿真。为简化分析过程，在对于EUVG表面形貌进行建模仿真时做出如下假设：（1）砂带磨削过程中运动稳定；（2）磨削过程中磨粒不发生脱落与磨损；（3）超声振动在磨削过程中状态保持稳定。       

1.2超声振动辅助砂带磨削下表面形貌仿真

       本文假设砂带表面磨粒分布均匀，则磨粒之间的间隔距离∆可表示为：

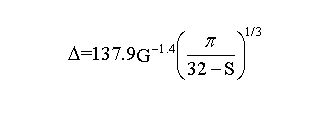
       其中G表示磨粒数，S表示结构数(在本文中G=80,S=2)。

       磨粒的中心点坐标为G(x0,y0,z0)，则磨粒的轮廓表示为：

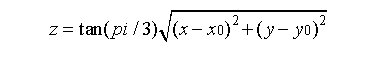
       磨粒的平均高度可表示为[28][29]：

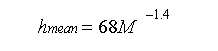
       其中M为砂带粒数。

       砂带磨粒中心的坐标为V(x,y,z)，圆锥体的中心点的坐标为G0(x0,y0,z0)，则

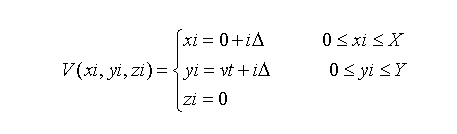
       其中X和Y分别为磨削表面在x和y方向的大小，∆为两点之间的间隔距离。

       考虑砂带的弹性磨削特点，由磨粒运动轨迹我们可得知圆锥体的中心点G0(x0,y0,z0)的表达式为：

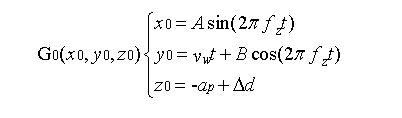
       ∆d为砂带磨削过程弹性磨削的位移，其中∆d≤σm·π(a_p)^2 (tan(θ/2))^2，σm为材料的流动压力：

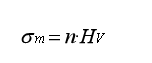
       其中HV是材料维氏硬度，n是与工件之间的相互作用，通常n=1.08。

       第i颗磨粒的中心的的表达式为：

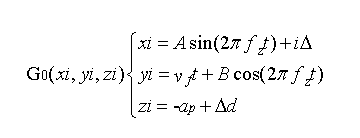
       即圆锥体的中心点沿磨粒磨削轨迹运动并对工件表面产生材料去除，Z为圆锥体在工件表面加工后的轮廓值，选取在该空间磨粒轮廓的最小值作为磨削表面的轮廓H可表达为，

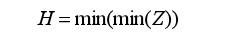
       2.1 仿真结果分析

图2.1所示为不同振幅下使用MATLAB仿真的表面形貌。由于磨削轨迹重复率随着轴向振幅A和切向振幅B的增加而提高，因此磨削后残余面积的高度会降低，且能够提高表面粗糙度和光洁度。

图2.1不同振幅对于表面形貌的影响（vf=5 mm/s）

       3.结论

       （1）使用MATLAB对椭圆超声振动磨削表面形貌进行仿真分析，并通过实验验证模型的可靠性。

       （2）随着轴向振幅A的增加，磨削纹理的打断效果更佳，表面粗糙度降低。切向振幅B的增加对表面形貌的影响主要表现为，重复磨削区域增加，磨削表面光洁度有所提高，表面粗糙度减小。但对纹理特征并没有明显的影响。