磨料磨具网

       砂带磨削是砂带这一特殊形式的磨削工具，借助于张紧机构使之张紧，和驱动轮使之高速运动，并在一定压力作用下，使砂带与工件表面接触以实现磨削加工的整个过程。

       砂带磨削是木质材料加工技术中尤为重要的一项。砂光机占木材加工设备总数的4％左右，而磨削加工占木质材料切削加工的30％左右，磨削能耗占总加工能耗的15％ ～25％。

       磨削的主要目的是定厚（尺寸校准）、去除人造板表面的预固化层等，对木质材料产品的加工精度、表面质量和胶合质量具有至关重要的作用。

       目前关于木质材料磨削加工的理论不足，磨削工艺参数和动力配置不合理，从而导致磨削加工能耗高、产品质量差及磨削机械设计不合理等问题，急需木质材料磨削加工理论研究指导实际磨削生产，以提高材料利用率和产品质量，降低生产能耗。

       磨削参数及木材性质都影响磨削力和磨削功率，且木材砂带磨削过程的变异性较大。用常规回归分析法建立经验模型较为困难，适用范围较窄，需要建立广泛适用的数据模型。

       磨削加工包括滑擦、耕犁和切削3个过程。当工件上的压力非常小时，磨粒只会擦拭工件表面；当压力略有增加，砂带磨削开始耕犁和切削木制品表面。滑擦、耕犁和切削的比例反映了单位面积砂带参与磨削磨粒的量，不同的比例也会导致磨削能耗发生变化。可以通过合理配置磨削参数，增加磨削过程中有效切削的比重。但在实际生产中，切削阶段只能通过间接的方式测定。磨削力是磨削加工中最基本的输出信号，几乎影响所有磨削现象。

       本研究从磨削力做功出发，采用磨削功率利用率μ（即磨削力做功功率Pst占整个磨削功率Ps的百分比）来间接反映磨削能耗利用效率。

       磨削力包括滑擦、耕犁和切削阶段所产生的力，所以磨削力做功基本可以体现磨削过程中材料的弹塑性变形以及切除材料的耗能。若磨削功率利用率大，则可间接说明磨削力做功主要作用于切削阶段，即产生材料切除，而滑擦与耕犁阶段的磨削热占总能耗的比例小；若磨削功率利用率小，则可间接说明磨削力做功主要作用于滑擦和耕犁阶段，即磨削热和空气阻力、噪声等其他能耗占总能耗的比例大。

       综上，北京林业大学应俊华，罗斌等重点研究不同磨削工艺参数对实际材料去除效率的影响，体现为磨削力做功在整个磨削能耗中的占比，从而优化磨削工艺参数，指导实际生产，提升能源利用效率。

       1 材料与方法

       1.1　试验材料

       1.2　试验方法

       1.3　测试方法

       2 结果与分析

       2.1　砂带磨削参数对砂光机空转功率的影响

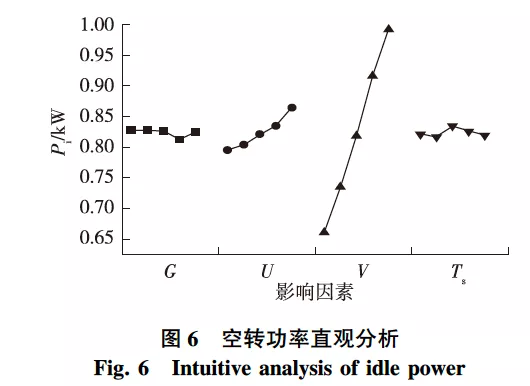
       对影响砂光机在空转时有功功率（以下简称为空转功率）的磨削参数进行方差分析可知，各参数对空转功率的影响顺序为V＞U＞Ts＞G，砂带速度和进给速度对空转功率有高度显著影响，而砂带磨料粒度和磨削深度与空转功率的相关性不大。对空转功率的直观分析见图6。由图6可知，空转功率随着砂带速度和进给速度的增加基本呈线性增加，且增加最明显的是砂带速度。改变砂带速度和进给速度时，空转功率的水平极差分别为0.331和0.069kW，水平极差之比约为5。空转功率的变化规律反映了试验所用砂光机的部件电机能耗，即砂带转动电机功率大于试件进给电机功率。此外，砂带速度对空转功率的影响较大也与其引起的风阻较大有关，砂带转动时受到的空气阻力（f）满足空气阻力公式：

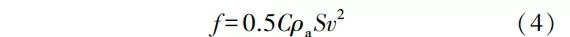
       式中：C是阻力系数，Pa是空气密度，S是物体有效横截面积，v是物体移动速度，此处与砂带速度相同。由式（4）可知，空气阻力与砂带速度呈二次方的关系，砂带速度越大，受到的空气阻力越大，能量损耗越大。而磨料粒度和磨削深度对空转功率无影响，侧面反映了试验结果的稳定性和可靠性。

       2.2　砂带磨削参数对杨木和红松Psf和μ的影响

       砂带磨削参数对杨木和红松Psf和μ的影响正交试验方差分析见表2。由表2可知，4个因素都是高度显著影响Psf的因素，顺序为U＞Ts＞V＞G。磨削参数对μ影响的大小顺序为Ts＞G＞V＞U，其中，G和V为显著影响因素，提高砂带磨削木质材料的功率利用率，主要从改变Ts、G和V的大小出发。Ts和G对Psf和μ均为高度显著影响，这反映了砂带磨削木质材料的影响规律，随着Ts的增加，磨削总量增加，每齿切削量增加，磨削力增大，磨削力做功功率增大。而G可反映磨料粒度和磨粒数目，直接影响每齿切削量，进而影响磨削力，对整个磨削过程的磨削力做功功率产生高度显著影响。磨削参数U和V都是Psf的高度显著影响因素，且仅改变U，对Psf影响最大；此外，U可以影响单位时间内磨削木质材料的长度，改变U就可改变单位时间内的磨削量，影响磨粒每齿切削量，进而影响磨削力和Psf的大小。根据式（1），V的增大会导致Psf增大， 但是V的增大也会使单位时间内磨削木材的总磨粒增多，参与切削的磨粒数目增加，每齿切削量减少，磨削力减小，从而使Psf值减小。因此，V对Psf的影响小于U。

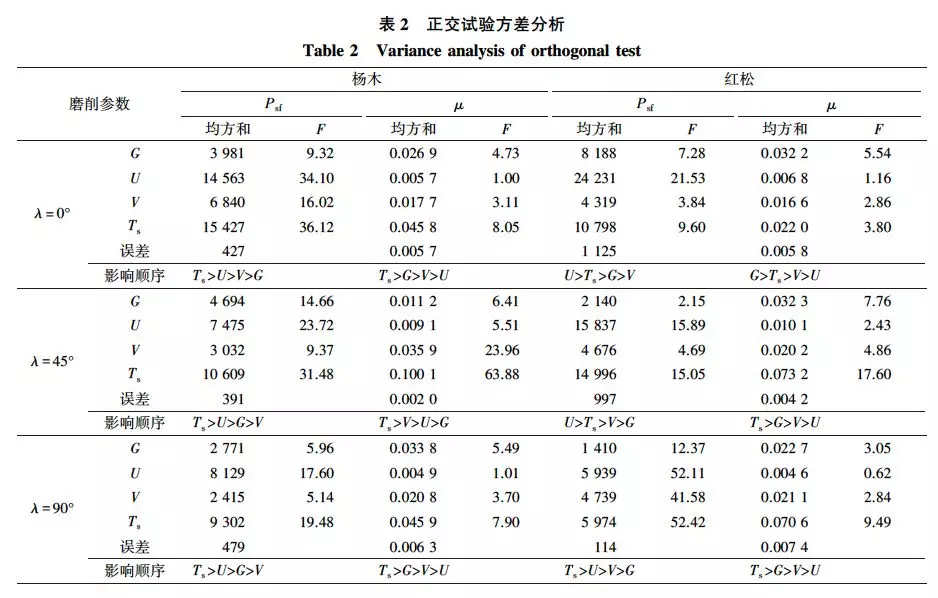
       顺纹磨削时，Ps和G是影响μ的主要因素，V和U则对μ几乎没有影响。杨木顺纹磨削时，Ts是μ的高度显著影响因素；而红松顺纹磨削时，Ts的F值只是接近显著影响因素。斜纹磨削时，杨木斜纹的不同磨削参数F值大多比红松斜纹磨削时大。杨木斜纹磨削时，Ts和V是高度显著影响因素，G和U是显著因素；红松斜纹磨削时，Ts和G是高度显著影响因素，V是显著因素，U对μ无影响。横纹磨削时，2种木材的Ts都为高度显著影响因素；杨木的G为显著影响因素，红松的G则对μ无影响；红松与杨木相比，改变磨削参数U和V时，红松对μ的影响更小。μ在杨木顺纹、斜纹和横纹磨削时得到的总数据中的极差分别为0.148，0.195和0.158；在红松顺纹、斜纹和横纹磨削时分别为0.149，0.183和0.168。因此，改变磨削参数时，μ的总改变量从大到小依次为杨木斜纹、红松斜纹、红松横纹、杨木横纹、红松顺纹、杨木顺纹。对于同种木材，μ值的变化量：斜纹＞横纹＞顺纹。杨木磨削时，μ的改变量略大于红松。红松的密度和表面硬度都比杨木大，且纹理排列更单一，同种磨削参数磨削时，硬度和密度更小的木材μ 值的变化量更大。磨削参数对Psf影响的直观分析图见图7。由图7可知，Psf的值随各参数值的增大而增大。G对Psf值的影响，除顺纹磨削时仅有60目1个拐点；斜纹及横纹磨削时分别在60和100目都有2个拐点。随着U的增大，Psf逐渐增大，且增大的速度也逐渐增加。随着磨削参数V和Ts的增加，Psf基本呈直线增大。在不同纹理时的最大值不同，杨木顺纹、斜纹和横纹磨削时的Psf最大值分别为0.34，0.26和0.24kW；红松顺纹、斜纹和横纹磨削时的Psf最大值分别为0.35，0.32和0.23kW。磨削力做功功率大小顺序为顺纹、斜纹、横纹。磨削参数对μ影响的直观分析见图8。由图8可知，随着磨削参数Ts的增加，μ呈下降趋势；Ｇ增大时，μ的值也基本呈下降趋势，斜纹和横纹磨削时，在60和100目处有2个拐点，红松顺纹磨削时仅有100目1个拐点，杨木顺纹磨削时则无拐点；磨削参数Ｕ增加时，μ呈先减小后增大的凹形；磨削参数Ｖ增加时，μ基本呈上升趋势。这表明顺纹磨削时，采用40目砂带更有利于提高磨削功率的利用率，而斜纹和横纹磨削时采用60目砂带更优。采用高速磨削可提高磨削功率的利用率，使用最高进给速度或最低进给速度可稍微提高μ值；在同样的磨削条件下，随着Ts的增加，μ在整体上呈降低趋势，Ts越大，实际磨削深度与设定厚度偏差越大。此外，磨削不同的树种，在不同纹理方向下，最高磨削效率都不相同。根据各纹理方向下的μ数据汇总，杨木顺纹、斜纹和横纹磨削时的μ平均值分别为0.425，0.442和0.510，红松顺纹、斜纹和横纹磨削时的μ平均值分别为0.366，0.542和0.420。磨削效率的高低顺序为红松斜纹、杨木横纹、杨木斜纹、杨木顺纹、红松横纹、红松顺纹。杨木磨削效率顺序（横纹＞斜纹＞顺纹） 与前人研究结果相同，而红松则为斜纹＞横纹＞顺纹。红松斜纹磨削效率更高，这是因为针叶材的纹理相比杨木这类阔叶材更通直。对各磨削参数下μ的直观分析，可得最佳功率利用率（高磨削效率）的磨削方案为：磨削深度0.1mm，砂带速度10.74m/s，进给速度5.16m/min，磨料粒度60目，杨木横纹磨削，红松斜纹磨削。经计算，平均功率利用率45％，最大功率利用率78％，最小功率利用率21％。

       2.3　杨木砂带磨削参数的BP（back propagation）神经网络建模　　

       本研究采用单隐层的BP神经网络系统对杨木的纹理、磨削参数与Psf和μ2种表征量之间的非线性关系建立仿真模型，该中间层神经元数目（隐层节点数）可以根据kolmogorov定理选择：

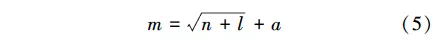
       式中：m是隐层节点数；n是输入节点数；l是输出节点数；a是1～10间的常数。具有单隐层的BP神经网络可以映射所有连续函数，只有当学习不连续函数时才需要2个隐层。因此，本试验选用单隐层的BP神经网络。增加隐层节点数，网络从样本中获得信息的能力会有所提高；但如果隐层节点数过多，网络又可能把样本中非规律性的内容（如噪声）记牢，反而降低了泛化能力，也会使训练时间增加。当样本数固定时，较少的隐层节点数可能无法表达所有的样本规律。当样本数目过少时，有较多隐层节点数的神经网络得不到有效训练。经过反复测试，本试验的隐层最终选用3节点。输入层（Ｇ、Ｕ、Ｖ、Ts和λ）是五维的向量，所以输入层为五节点。输出2个结果（Psf和μ）为二维，所以输出层为两节点。BP神经网络的基本架构和调用函数通过以下代码完成：

       其中，“threshold”规定输入向量的最小值（0）和最大值（1），“tansig” 为网络中间层传递函数tansig（），输出层传递函数为对数函数logsig（），训练函数为trainlm（）。木质材料磨削过程影响结果比较复杂，适当增加训练次数和减小学习速率，可以提高训练准确度。网络训练次数设置为1000次，学习速率设置为0.01，训练目标误差为0.001（0.1％），训练代码如下：

       将归一化后的试验参数和结果输入到代码中，得到训练代码并训练。进行BP神经网络预测，然后绘制预报误差曲线，训练代码如下：

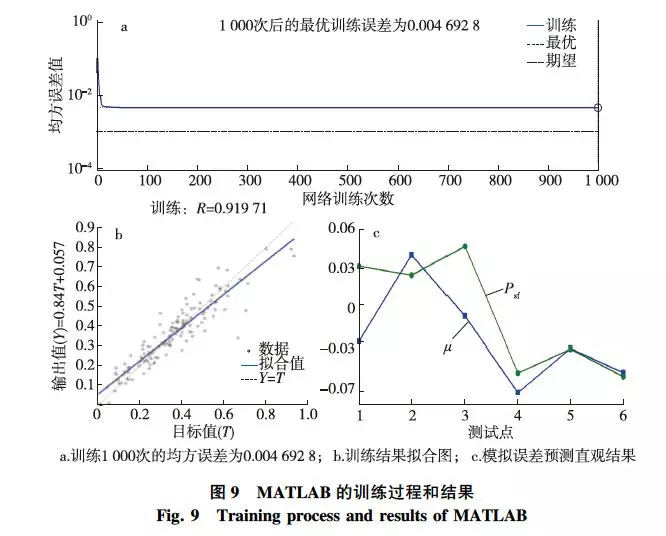
       BP神经网络的模拟结果见图9。由图9a可知，设置期望误差为0.001，实际1000次训练后可得均方误差为0.004 692 8；图9b显示了神经网络输出值与目标值（T）之间的拟合结果，可知：拟合结果的置信度约为92％，可以满足预测的基本要求；图9c为预测时网络输出结果与原数据的模拟误差值，可以看出，最大误差约为7％。

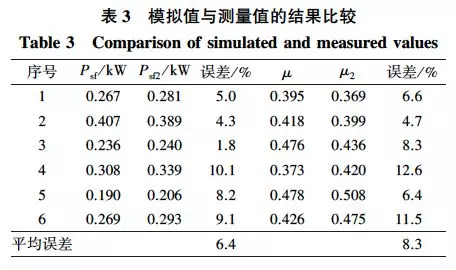
       模拟值与测量值的结果比较见表３。表３ 中Psf和μ表示测量值，Psf２和μ２表示模拟值。Psf的最大相对误差为10.1％，平均误差为6.4％；μ的最大相对误差为12.6％，平均误差为8.3％，完全可以满足砂带磨削杨木时Psf和μ的预测需要。本次预测时间小于2s，因此，BP神经网络系统减少了分析计算时间。由于木材材质本身的各向异性和多孔性，磨削结果跟金属等材料有很大区别，木材磨削中有测量结果误差大和数据噪声大等缺点，因此，建立Psf和μ的理论与经验模型较难。而BP神经网络具有良好的非线性映射能力、泛化能力和容错能力，可以满足木质材料磨削的实际建模和预测。

       结 论

       １）磨削参数对Psf的影响顺序为Ｕ＞Ts＞Ｖ＞Ｇ，且都为高度显著影响因素，对μ的影响顺序为Ts＞Ｇ＞Ｖ＞Ｕ，Ts为高度显著影响因素，G和V为显著影响因素。因此，提高砂带磨削木质材料的功率利用率，主要考虑改变Ts、G和V3个磨削参数。

       ２）Ts和G是影响Psf和μ的高度显著影响因素，Ts的影响最大，G次之。木材纹理对μ的影响，杨木磨削时从大到小依次为横纹、斜纹、顺纹，而红松则为斜纹、横纹、顺纹。

       ３）最佳功率利用率（高磨削效率）的磨削方案为：磨削深度0.1mm，砂带速度10.74m/s，进给速度5.16m/min，磨料粒度60 目，杨木横纹磨削，红松斜纹磨削。平均功率利用率45％，最大功率利用率78％，最小功率利用率21％。

       ４）采用BP神经网络建立杨木的Psf和μ仿真模型，拟合结果的置信度约为92％，实际预测中Psf的平均误差为6.4％，μ的平均误差为8/3％，可以满足预测的基本要求。

       该文发表于《林业工程学报》2019年第3期。